Free body diagram
Free body diagram: A special type of vector diagram used to study the magnitude and direction of forces acting on body
Free Body Diagrams
A way of analysing the static forces and moments acting on a joint, FBD is a 2d simplification of a 3d structure
It is a static analysis (inertia – Newton’s first law)
All other variables must be equal to zero
6 variables are present
• Force in the x, y and z axes
• The moments created in these axes
Seven assumptions are made when using free body analysis
(JOIN BMW)
1. Joints are frictionless hinges
2. Only compressive forces act on joints
3. Internal forces are equal - therefore not analysed (within the body)
4. No antagonistic muscle action
5. Bones are rigid rods
6. Muscular force is in the direction of the muscle belly
7. Weight of the body is concentrated at the centre of the body mass
Also remember
Body we draw should be in equilibrium
There are no antagonistic muscles
Muscle act only through tendon
JRF is always compressive
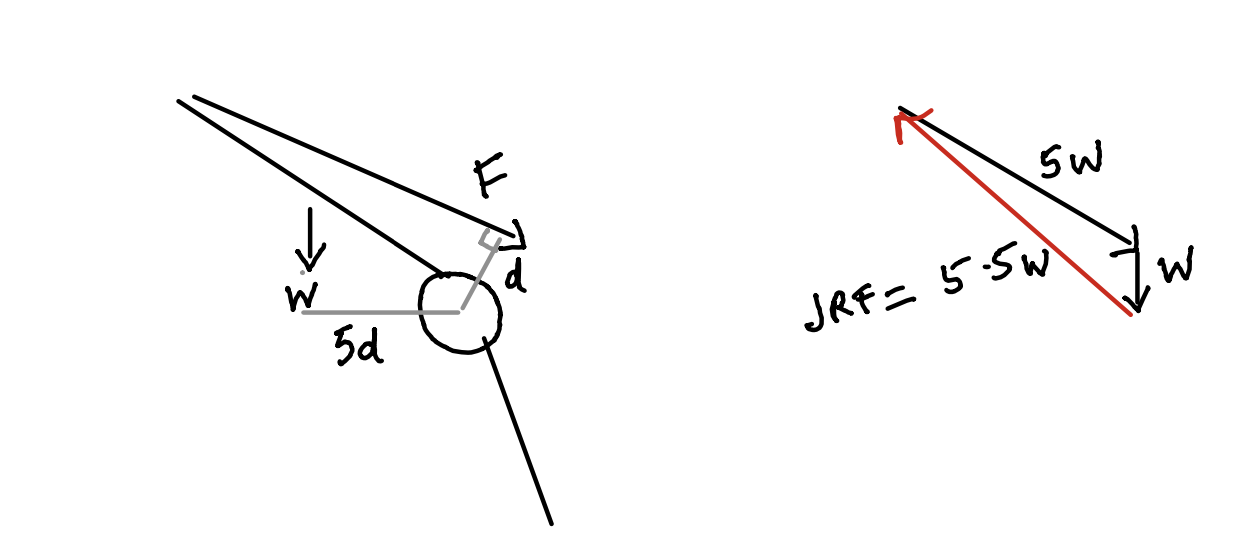
Hip FBD
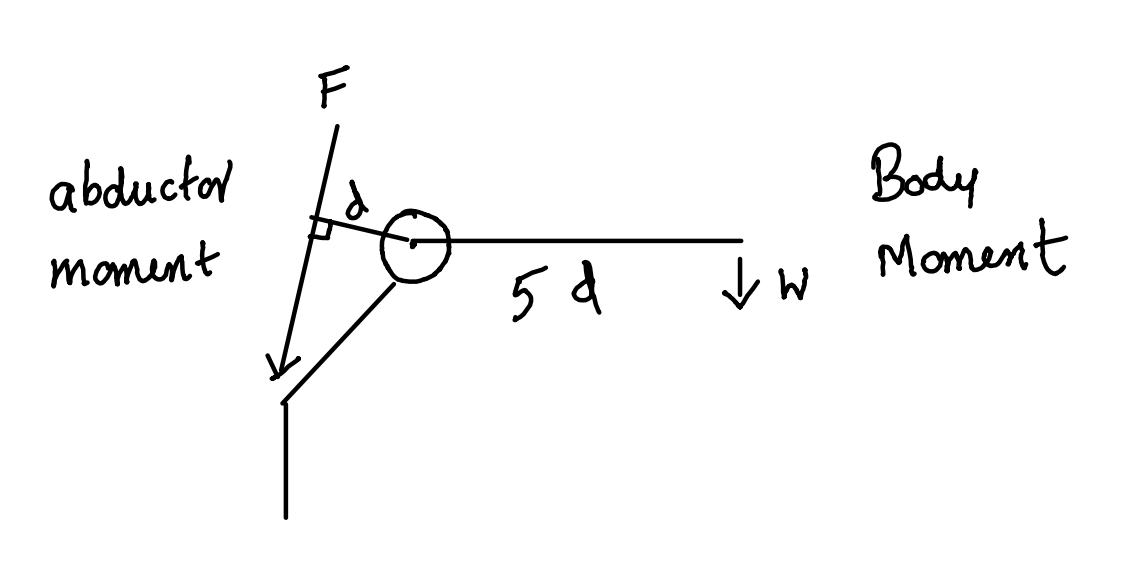
Abductor moment = body moment in equilibrium
Fd = w x 5d
F = 5w
*w is generally taken as 5/6 of the body weight as the person is standing on one leg. Weight of one leg is generally taken a 1/6 body weight.
*F is the abductor force of contraction.
JRF
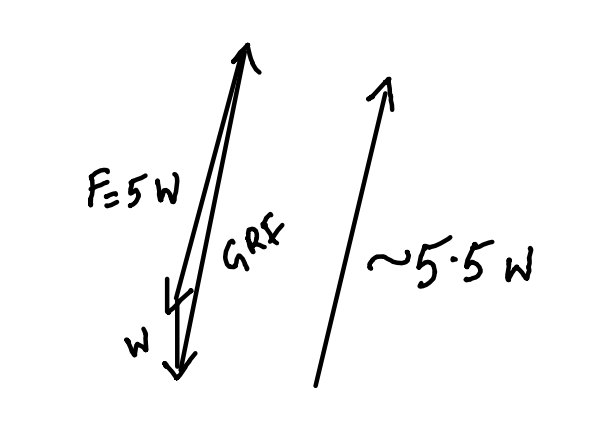
How to reduce JRF in hip?
Carry weight on same side!
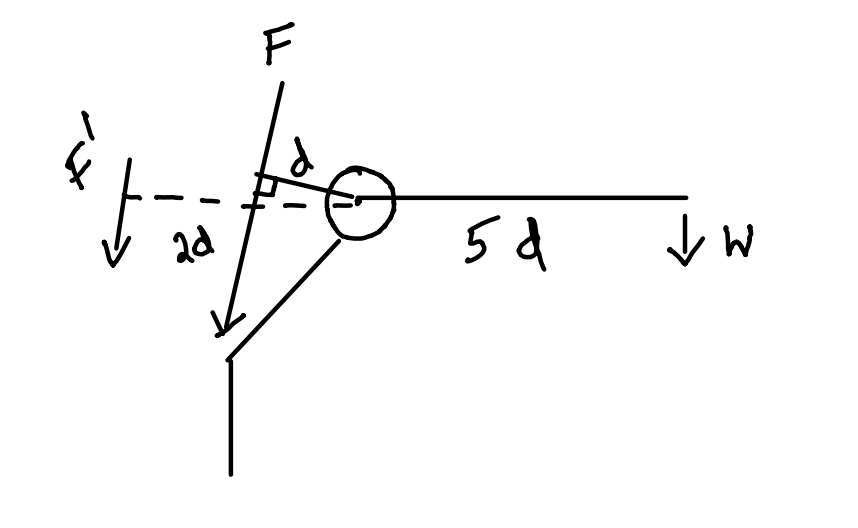
F x d + F’ x 2d = w x 5d
F + F’ = 5w
F = 5w - F’
So the abductor force of contraction required is reduced from F to F-2F’
Carry stick on the opposite side!
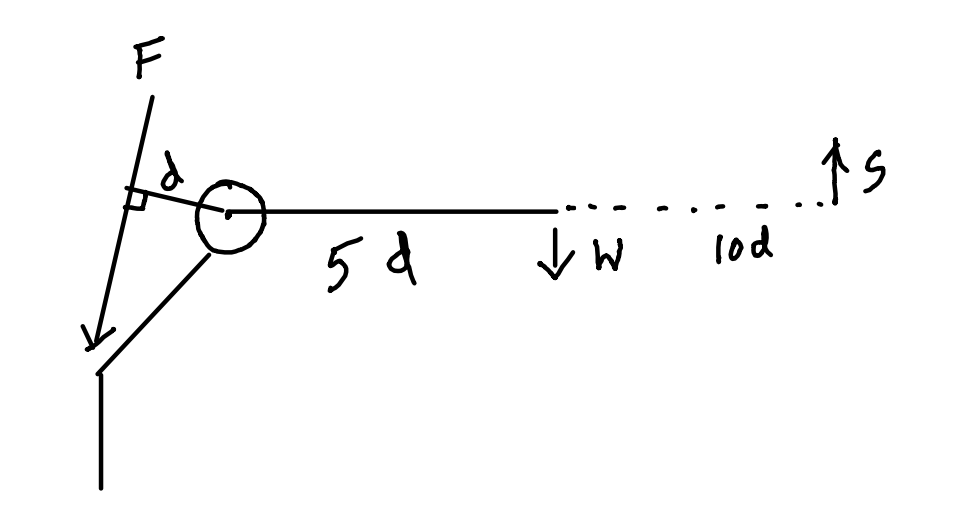
Pressing the stick on to the ground will produce an equal and opposite ground reaction force, s.
F x d = w x 5d - s x 10d
F = 5w - 10s
So the abductor force of contraction required is reduced from F to F-10s
Ankle FBD
It is important to keep the ankle in dynamic equilibrium
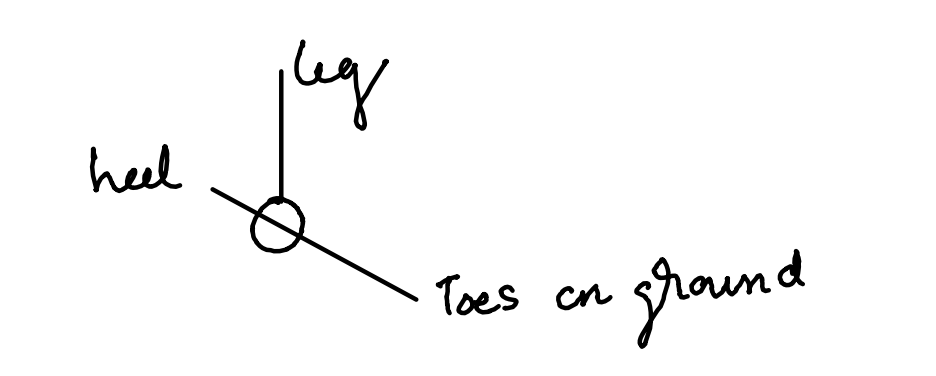
This essentially make ankle a reverse hip joint, another type one lever
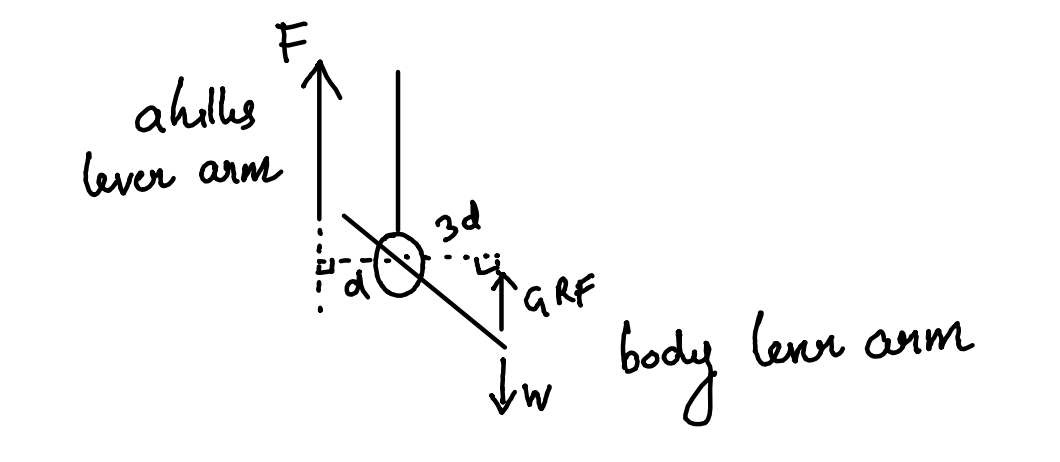
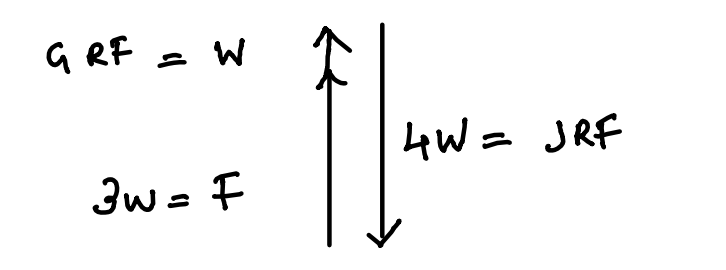
F x d = w x 3d
F = 3 w
JRF ankle
Spine FBD
Assume a man bending forward and trying to take a brick. Here the motion segment is again acting as a type 1 lever.
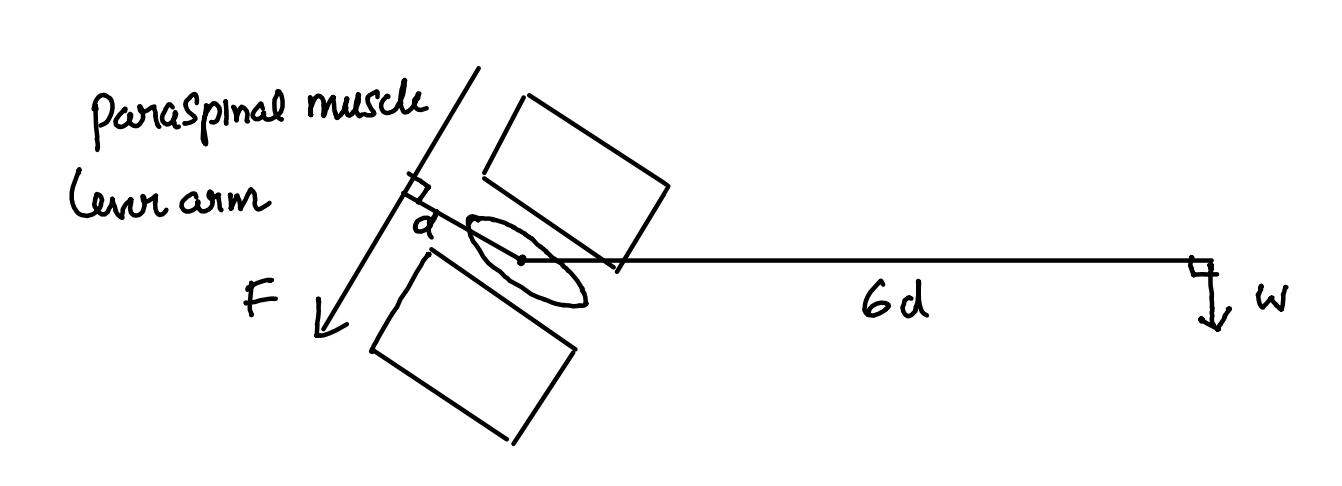
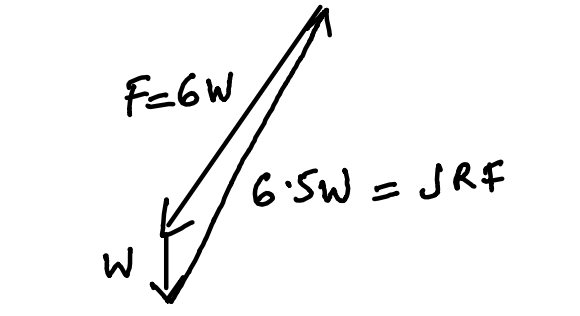
JRF Spine
Cervical Spine FBD
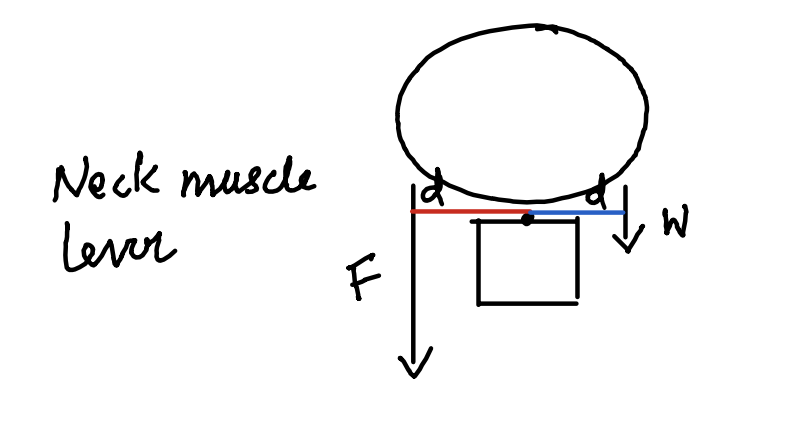
F x d = w x d
F = w
Patello femoral joint FBD
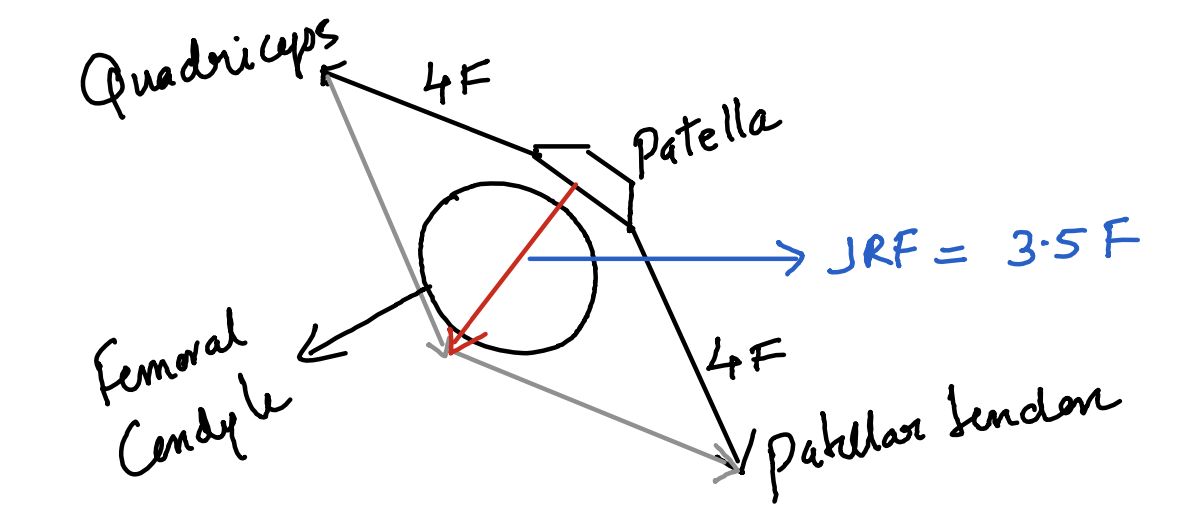
The quadriceps and patellar tendon are in equilibria, with a force 4F on either direction. The JRF is less than 4F. JRF is maximum when in flexion and negligible in extension of knee joint.
Knee joint FBD
We can see that when a person is about to raise from a chair, knee joint acts as a second order lever. Weight is acting down from the middle of the thigh and the quadriceps force F is directed towards the knee.
Shoulder joint FBD
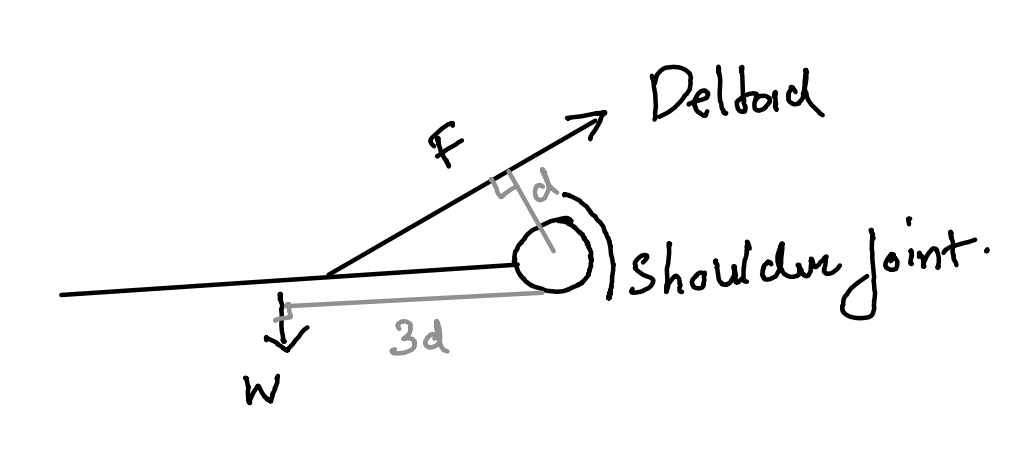
Here we can see that shoulder is a third order lever.
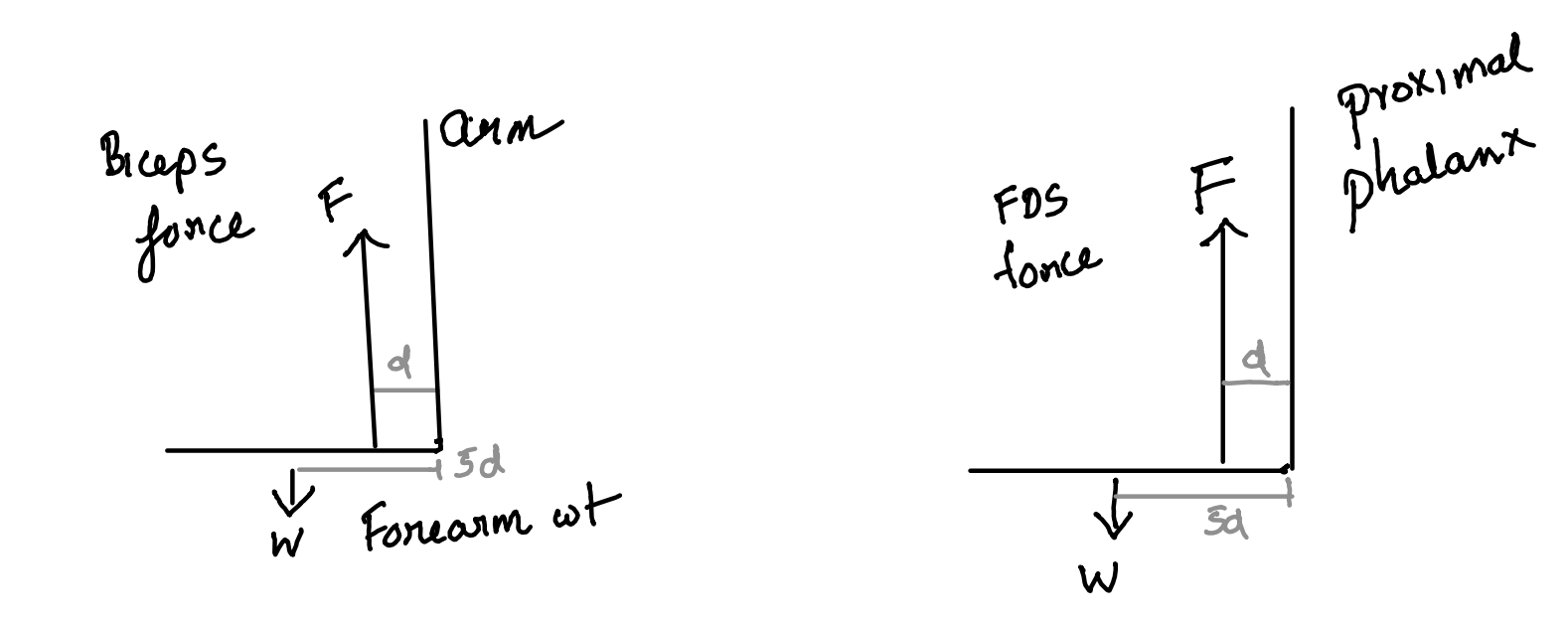
Elbow and fingers FBD